Aktuality

Ing. Marek Pátý, Ph.D. měl asi štěstí na dobré učitele matematiky, ale ke vztahu k matematickému modelování se musel dopracovat sám. Vystudoval Fakultu strojní ČVUT v Praze na Ústavu technické matematiky a jako člen týmu studentské formule eForce FEE Prague Formula navrhoval design a aerodynamické prvky monopostu FSE.03. A matika ho pořád baví. Používá ji v práci i v soukromém životě.

Více o tom řekne sám Marek v krátkém rozhovoru:

 
Mnoha studentům středních škol připadá matematika jako strašák. Myslíte, že je to tím, že mají chatrné základní vědomosti a začali se matiky bát dřív, než pochopili její principy a možnosti? Anebo je to jen lenost myslet a pracovat?
Porozumění matematice klade vysoké nároky na logiku, analytické uvažování a představivost. Pokud někdo nemá v tomto směru nadání, je pro něj nesnadné do matematiky proniknout i při sebevětší píli. Matematiku se lze jen obtížně učit samostudiem, minimálně zpočátku. Mnohem snazší je, pokud Vám někdo problematiku dokáže názorně a srozumitelně vysvětlit. Velkou pomocí je tedy mít dobrého učitele.

Sblížili Vás s matikou učitelé? Nebo co Vás přesvědčilo, že matika je užitečná pro profesionální i osobní život a může i bavit?
Na matematice mě vždy nejvíce bavilo řešení problémů. Pocit, když si nad něčím dlouho lámu hlavu a pak naleznu řešení, je pro mě silně návykový. Stejně to mám s programováním, když se mi podaří najít chybu v kódu a program začne správně fungovat.

Na co jste se při studium matematiky na Fakultě strojní nejvíce zaměřil?
Pro technické výpočty je v dnešní době nejdůležitější numerická matematika. S její pomocí jsme schopni přeformulovat komplikované matematické problémy tak, aby je dokázal řešit počítač. Typicky místo původní složité diferenciální rovnice získáme soustavu lineárních rovnic, která je principiálně mnohem jednodušší na řešení. Obsahuje však často desítky či stovky milionů neznámých, a proto už ji nejsme schopni řešit na papíře, ale musíme se spolehnout na hrubou výpočetní sílu. Já se konkrétně zabývám výpočty proudění, především v parních turbínách a v leteckých motorech.

Po promoci na Fakultě strojní jste pokračoval ve studiu na Von Karman Institut pro dynamiku tekutin v Belgii. Věnoval jste se tam také nějakým projektům?
Na VKI jsem absolvoval roční studijní program Research Master, jehož podstatnou část tvoří vedle docházení na přednášky právě práce na nějakém výzkumném projektu. Skvělé na tom je, že jde o špičkové projekty, které typicky vznikají na základě poptávky nějakého partnera VKI z průmyslu. Nejsou to tedy projekty „do šuplíku“, které by studenti dostávali jen proto, aby vykázali nějakou činnost. Já jsem pracoval na optimalizaci tvaru špičky lopatek ve vysokotlaké turbíně leteckého motoru. Na základě tohoto výzkumu vzešlo další téma, kterému jsem se následně věnoval - metody pro identifikaci vírů v proudovém poli.
 

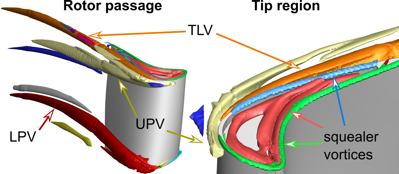Pobyt na zahraniční univerzitě byl asi přínosný. Počítáte s dalším získáváním zkušeností v zahraničí?
Po studiu na VKI jsem se vrátil na Fakultu strojní, abych dokončil doktorát, což se mi ale oproti původním plánům trochu protáhlo. S odstupem času na program Research Master nahlížím jako na nejcennější studijní a profesní zkušenost a rozhodně plánuji zase vycestovat, jakmile to rodinná situace dovolí.

Na jaké téma jste zaměřil doktorskou práci?
Věnoval jsem se řešení samovolného kmitání turbínových lopatek, které se nazývá flutter. Vlivem interakce s okolním prouděním se lopatka může rozkmitat, což následně vede k její deformaci nebo dokonce utržení. Problém flutteru se poprvé začal intenzivně řešit při návrhu křídel letadel před druhou světovou válkou, ale může postihnout i lopatky kompresorů a turbín. Ve své práci jsem se zabýval řešením tohoto jevu u špiček lopatek nízkotlakého stupně parních turbín. Zde je situace komplikována tím, že proudění může být na vstupu do lopatkového kola nadzvukové, což vede ke vzniku rázové vlny před lopatkou. Je proto obtížné formulovat okrajové podmínky tak, aby nevytvářely nefyzikální odrazy této vlny a nenarušovaly tím řešení proudění.
 

Budete své téma rozvíjet v dalším studiu anebo ve výuce?
Téma flutteru prozatím opouštím a začínám pracovat na připravovaném projektu FS, který se týká pokročilých technologií pro udržitelné letectví. Budu navazovat na svou práci na VKI, týkající se vírů v proudovém poli. Plánuji pokračovat ve vývoji nástroje pro automatickou identifikaci a popis vírů a zkoumat, zda lze vytváření vírů aktivně řídit a zlepšit tak například aerodynamické vlastnosti letadla či účinnost jeho motorů.
 

Považujete v technických vědách za důležitější matematiku anebo fyziku?
Při řešení technických problémů jsou fyzika i matematika nezastupitelné a vzájemně provázané. Znalost fyziky je nezbytná pro sestavení modelu problému a stanovení, jaké jevy hrají významnou roli a které si naopak můžeme dovolit zanedbat. Bez matematiky bychom ale problém nedokázali přesně formulovat a následně vyřešit.
 

Jak byste přesvědčil zájemce o studium, že matematika je užitečný a zajímavý nástroj pro každou technickou profesi?
Bez technických výpočtů, jako jsou simulace proudění CFD nebo pevnostní analýza FEM, se dnes neobejde návrh prakticky žádného jen trochu složitějšího strojírenského výrobku. Používají se při nich softwarové nástroje, které jsou koncipovány uživatelsky přívětivě, aby je dokázalo používat co nejvíce lidí. Zdánlivě tedy není potřeba hlubší znalost matematicko-fyzikálního modelu, na němž je program založen. V praxi to ale znamená, že k nějakému výsledku sice dospěje každý, ale ten výsledek může být špatně. Výpočtářské firmy proto už v dnešní době kladou na znalosti matematického modelování značný důraz. Ve výsledku je pro ně výhodnější zaplatit více člověku, který dokáže správně nastavit výpočet a posoudit správnost výsledků, než platit méně tomu, na jehož výsledky se nelze spolehnout.
 

Myslíte, že i v osobním životě mohou někdy pomoci znalosti matematického modelování a ověřování výsledků simulací?
Domnívám se, že alespoň základní znalost matematiky a matematického myšlení je pro orientaci v dnešním světě nezbytná. To bylo názorně vidět při pandemii covidu, kdy se člověk bez správné interpretace počtu nakažených, denního přírůstku, reprodukčního čísla R a dalších parametrů mohl v informacích z médií lehce ztratit. To pak svádí ke zjednodušení a k extrémním názorům, že covid je buď neškodná chřipečka, nebo naopak důvod k naprosté panice. Křivka nakažených teď alespoň může dobře posloužit učitelům matematiky jako příklad při probírání exponenciální funkce. Mně se třeba momentálně matematické modelování hodí k jednoduchému propočtu návratnosti fotovoltaické elektrárny a optimalizaci jejích parametrů.