Aktuality

Zveme vás na přednášku GRANSO: softwarový 'open-source' nástroj pro náročné optimalizační úlohy s využitím metody BFGS-SQP.

GRANSO: An Open-Source Software Package Employing a BFGS-SQP Method for Constrained, Nonsmooth, Nonconvex Optimization.

Přednášející

Dr. Tim Mitchell (mitchell@mpi-magdeburg.mpg.de), Max Planck Institute for Dynamics of Complex Technical Systems; Computational Methods in Systems and Control Theory; Magdeburg, Germany.

Přednáška se koná 5. června 2017, od 10.00 hodin v konferenčním sále ( místnost C1-17, přízemí) Fakulty strojní ČVUT v Praze, Technická 4, Praha 6 a proběhne v angličtině.

Date: 5. 6. 2017, 10:00; Place: Conference room No. 17 – Faculty of Mechanical Engineering, CTU in Prague, Technická 4, Prague 6

Abstrakt

V přednášce bude představen 'open-source' softwarový nástroj GRANSO (GRadient-based Algorithm for Non-Smooth Optimization) pro náročné optimalizační úlohy s omezením v případech, kdy je kriteriální funkce nekonvexní a její gradient může být lokálně nespojitý. GRANSO je aktuálně jedním z mála dostupných softwarových nástrojů pro daný typ optimalizačních úloh. Po teoretickém úvodu s přehledem aplikovaných optimalizačních principů, bude následovat demonstrace použití nástroje GRANSO v prostředí Matlab na řadě praktických úloh.

Abstract

We present a new open-source software package for solving nonsmooth, nonconvex, constrained optimization problems as well as two new open-source packages for benchmarking: a new test set of 200 challenging nonsmooth constrained optimization problems and new visualization tools for comparing the relative performance of optimization algorithms.  Although nonsmooth optimization is a well-studied area, there is still little available software specifically designed to handle general nonsmooth constraint functions.  In 2012, Curtis and Overton proposed a relevant gradient-sampling-based SQP method, proving convergence results under the assumption that the objective and constraint functions are locally Lipschitz, but the many gradient evaluations needed per iteration can make the method quite slow in practice.  Our new solver, called GRANSO: GRadient-based Algorithm for Non-Smooth Optimization, is instead designed to use few function/gradient evaluations per iteration.  While GRANSO's underlying algorithm has no convergence guarantees, we have nonetheless observed that it performs very well in practice on difficult nonsmooth optimization problems, where the objective/constraint functions are either locally Lipschitz or non-locally-Lipschitz and where the constraints are typically both active and nondifferentiable at local minimizers.  In this talk, we motivate and present GRANSO's underlying BFGS-SQP algorithm and then describe our new test set of problems and visualization tools we used to empirically validate GRANSO's performance against alternative methods.

Joint work with
Frank E. Curtis - Lehigh University
Michael L. Overton - New York University
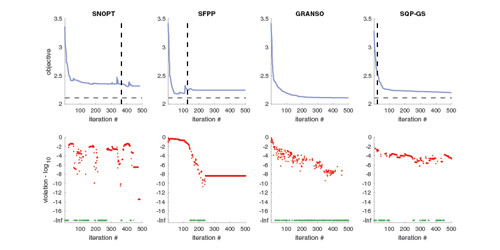Figure 1:
The plots show the progression of iterates from GRANSO and three other solvers on a nonsmooth nonconvex constrained optimization problem. 
 






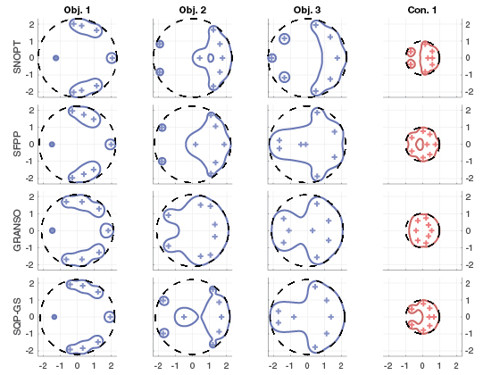
Figure 2:
The problem was to design a single controller matrix that would minimize the max epsilon-pseudospectral radius of three static-output-feedback (SOF) plants such that the epsilon-pseudospectral radius of a fourth SOF plant remained less than 1.
 

Bio

Tim Mitchell is a postdoctoral research scientist at the Max Planck Institute for Dynamics of Complex Technical Systems in Magdeburg, Germany, specifically in the Computational Methods in Systems and Control Theory group led by Peter Benner.  His main focus to date has been on computational aspects of robust control and stability analysis.  In addition to GRANSO, a solver for general nonsmooth constrained optimization, he has also developed new algorithms and software for fast computation and approximation of robust stability measures, such as the real stability radius and H-infinity norm.  Prior to joining the Max Planck Institute, he was an assistant research scientist at the Courant Institute of Mathematical Sciences at New York University, where he also obtained his PhD in computer science in 2014.
 

The lecture by Dr. Mitchell will be followed by a related talk by Vyacheslav Kungurtsev, Department of Computer Science and Engineering - Intelligent Data Analysis, Faculty of Electrical Engineering, CTU in Prague.

Title: Spectral Optimization for Design of Input Shapers

Abstract: Input shapers can mitigate undesired oscillations of a system, however when placed within a closed loop, can introduce unstable poles in the system. We present an optimization problem of designing the coefficients of an equally distributed time delay shaper so as to minimize the residual vibrations subject to a constraint that the spectrum is located entirely in the left half plane. Using specialized software for solving nonsmooth, nonconvex optimization problems, we demonstrate that efficacy of our approach on a simple system.

The current research has been performed within Czech Science Foundation project 16-17398S - Time delay compensators for flexible systems, coordinated by prof. Vladimír Kučera

Bio: Vyacheslav Kungurtsev was born in Russia in 1986 then immigrated to the United States in 1993. He received his B.S. in Mathematics from Duke University in 2007 and his PhD at UC-San Diego in 2013 in Computational Mathematics. Subsequently he worked for one year as a postdoctoral fellow at KU Leuven, and then has since been a postdoctoral fellow at FEL in CVUT in Prague. His interests span nonlinear, nonconvex optimization algorithms, theory, and applications.